Latent Variable Models
Variational Auto-encoder
Variational Inference (VI)
VI의 목적인 posterior distribution($p_{\theta}(z|x)$)을 찾는 것이다. 여기서 $z$는 latent vector이다.
posterior distribution은 나의 obsesrvation이 주어졌을 때, 관심있어 하는 random variable의 확률분포이다.
조건이 바뀐 $p_{\theta}(x|z)$는 likelihood라고 부른다
하지만 일반적으로 posterior distribution은 구하기 어려운 경우가 많다. 그래서 posterior distribution에 근사하게 학습하는 variational distribution($q_{\theta}(z|x)$)을 최적화시키는 것이 VI의 최종 목적이 된다.
variational distribution에서는 KL divergence를 이용해서 loss를 최소화하여 posterior을 줄여보고자 한다.
$$\ln p_{\theta}(D) = \mathbb{E}_{q_{\phi}(z|x)}[\ln\frac{p_{\theta (x,z)}}{q_{\phi}(z|x)}] + D_{KL}(q_{\phi}(z|x)\parallel p_{\theta}(z|x))$$
※푸는 과정 따라가 보는 것을 추천
$\mathbb{E}_{q_{\phi}(z|x)}[\ln\frac{p_{\theta (x,z)}}{q_{\phi}(z|x)}]$를 ELBO라고 하고
$D_{KL}(q_{\phi}(z|x)\parallel p_{\theta}(z|x))$부분이 원래 줄이고싶던 objective(variational distribution과 posterior distribution 사이의 KL divergence)부분인데, 이 objective를 줄이는 방법이 어려우니 ELBO(Evidence Lower Bound)를 최대화 함으로써 objective를 줄이는 방법을 사용한다. 이것이 VI이다.
ELBO : Evidence Lower Bound
$$\mathbb{E}_{q_{\phi}(z|x)}[\ln\frac{p_{\theta (x,z)}}{q_{\phi}(z|x)}] = \int \ln \frac{p_{\theta} (x|z)p(z)}{q_{\phi}(z|x)} q_{\phi}(z|x)dz$$
$$=\mathbb{E}_{q_{\phi}(z|x)}[p_{\theta}(x|z)]-D_{KL}(q_{\phi}(z|x)\parallel p(z))$$
ELBO는 $\mathbb{E}_{q_{\phi}(z|x)}[p_{\theta}(x|z)]$은 reconstruction term이라 불리는 부분과,
$D_{KL}(q_{\phi}(z|x)\parallel p(z))$ prior fitting term이라고 불리는 부분으로 나뉜다.
여기에서 auto-encoder에서 reconstruction loss term에 해당한다.
prior fitting term은 적분을 포함한 KL divergence계산을 포함해서, 그 적분을 활용할 수 있는 isotropic Gaussian을 써서 나오는
$$D_{KL}(q_{\phi}(z|x)\parallel \mathcal{N}(0,l))=\frac{1}{2} \Sigma^{D}_{i=1}(\sigma^{2}_{z_{i}} + \mu^{2}_{z_{i}} - \ln(\sigma^{2}_{z_{i}})-1)$$
이 식을 loss function에 넣어서 학습을 진행하게 된다.
결국 이미지 입력 x를 잘 표현할 수 있는 latent space z를 찾고싶은 것이 목적이다.
z에 대한 확률분포 posterior를 잘 모르니까, variational distribution으로. encoder로 근사한다.
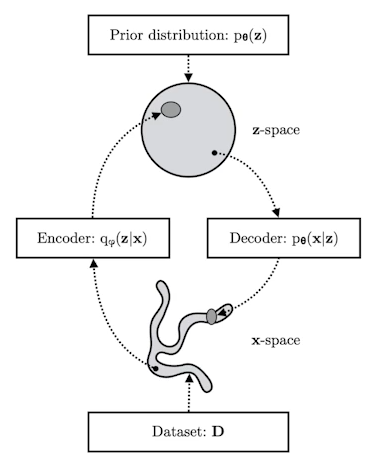
x라는 입력을 encoder를 통해서 latent space z로 보냈다가, 다시 decoder로 돌아오는 reconstruction loss를 줄이는 것이 reconstruction term이다.
prior fitting term은 많은 이미지를 latent space로 올려놓으면 하나의 이미지가 한 점이 될 것이다. 이 latent space에서 점들이 이루는 이미지들의 분포와 latent space의 prior distribution과 비슷하게 만들어주는 역할을 하는 게 prior fitting term이다.
그래서 variational auto-encoder는 implicit한 모델이다.
어떤 입력을 latent space로 보내서 무언가를 찾고, 그 무언가를 다시 reconstruction term으로 만들어지는데,
generative 모델이 되기 위해서는 prior distribution으로 z를 sampling하고, 그것을 decoder를 적용해서 나온 이미지 output들이 generation result라고 본다.
Variational Auto-encoder (VAE) 의 한계
- implicit, intractable model이어서 likelihood를 알기 어렵다.
- ELBO의 prior fitting term은 KL divergence계산이 있다. 그 KL divergence가 적분이 들어가 있기 때문에, ADAM으로 최적화를 시키기 때문에 미분이 가능해야만 한다. 그래서 가우시안을 활용해야만 한다.
Adversarial Auto-encoder
가우시안을 prior distribution으로 활용하고 싶지 않지 않을 때 AAE를 사용한다.
GAN을 이용해서 latent distribution 사이의 분포를 맞춰준다.
VAE의 prior fitting term을 GAN objective에 바꿔버린 것이다. 그래서 복잡한 분포들을 latent prior distribution으로 활용할 수 있게 되는 것이 장점이다.
성능도 VAE보다 가끔 좋을 떄가 많다.
GAN
generator 성능을 높히는 것이 목표인데, generator를 학습하는 discriminator가 점차 좋아지게 해서 generator 성능을 높힌다. GAN또한 implicit model이다.

Variational Auto encoder는 x라는 입력 이미지를 encoder를 통해서 latent vector z로 보내고, decoder를 통해 다시 x라는 domain으로 보내는 학습을 한다. generation 단계에서는 latent distribution에서 z를 sampling해서 decoder를 통과해서 나오는 x가 generation result가 된다.
GAN은 z라는 latent distribution에서 출발해서 Generator르 통해서 가짜 이미지가 나오고, discriminator은 generator에서 만든 가짜 이미지와 진짜 이미지를 구분하는 분류를 학습한다. 이렇게 학습된 discrimator입장에서 또 자신이 만든 fake image를 true로 착각할 수 있게끔 이미지를 generate하게 generator은 학습한다. 이 과정이 번갈아 가면서 generator과 discriminator이 학습하게 된다.
GAN Objective
높히고 싶어하는 discriminator와 낮추고 싶어하는 generator가 game을 하며 목표를 달성한다.
$$\min_{G}\max_{D}V(D,G)=\mathbb{E}_{x~p_{data}}(x)[logD(x)] + \mathbb{E}_{z~p_{z}}(z)[log(1-D(G(z)))]$$
이 식을 최적화 시키는 optimal discriminator은
$$D^{*}_{G}(x) = \frac{p_{data}(x)}{p_{data}(x)+p_{G}(x)}$$
을 만족시키게 된다.
generator가 고정되어 있을 때, $D^{*}_{G}(x)$값이 높으면 True, 낮으면 False로 분류된다.
이 optimal discriminator $D^{*}_{G}(x)$를 다시 generator에 넣으면
$$V(G,D^{*}_{G}(x)) = 2\times D_{JSD}[p_{data}, p_{G}]-log4$$
True data generative distribution과 내가 학습하고자 하는 generator사이의 Jenson-Shannon Divergence(JSD)를 최소화한다는 위의 식으로 정리된다.
이론적으로는 말이 되지만 현실적으로는 optimal distriminator가 수렴한다고 보장하기도 힘들다.
여러 GAN
- DCGAN
처음의 GAN은 multi layer perceptron을 사용한 dense layer로 만들었고,generator에는 deconvolution을, discriminator에는 convolution을 사용했다.
이미지 domain에 적용한 것이 DCGAN이다. - Info-GAN
학습할 때, 단순히 z로 이미지만 만드는 것이 아니라, random하게 class(random한 one hot vector)를 넣어서 generation을 할 때 GAN이 식으로 나오는 conditional one hot vector에 집중할 수 있게 만든다.
- Text2Image
문장이 주어지면 이미지를 만든다. - Puzzle-GAN
이미지 안에 sub patch를 통해 원래 이미지를 복원한다. - CycleGAN
이미지 사이의 domain을 바꾸어준다.
cycle-consistency loss를 사용한다. (중요한 개념) - Star-GAN
input을 control - Progressive-GAN
고차원의 이미지를 만들어낸다.
차근차근 저해상도에서 고해상도로 늘려나간다.
'부스트캠프 AI Tech 3기 > 이론 : U-stage' 카테고리의 다른 글
| [Day17] AI 서비스 개발 특강 1. 서비스 향 AI 모델 개발하기 (0) | 2022.02.15 |
|---|---|
| [Day17] AI 서비스 개발 2. 머신러닝 프로젝트 라이프 사이클 (0) | 2022.02.14 |
| [Day16] DL Basic 9. Generative Models - 1 : distribution, conditional independence, auto-regressive, NADE, pixel RNN (0) | 2022.02.10 |
| [Day15] DL Basic 8. Sequential Models - Transformer (0) | 2022.02.10 |
| [Day15] DL Basic 7. Sequential Models - RNN (0) | 2022.02.09 |

