Generative model 생성모델
- Generation
train data에 있지 않은 sample을 만들어내는 것
sampling으로 활용될 수 있다.
단순히 generate만 할 수 있는 모델이면 implicit model이라고 한다. - Density estimation
이미지가 알고있는 분류와 같은지 아닌지 예측하는 확률 p(x)을 얻어낼 수 있다 -> explicit model
anomaly detection으로 활용될 수 있다
구분할 수 있는 능력도 있다. - Unsupervised representation learning
feature learning
Basic Discrete Distributions
- Bernoulli distribution
서로 의존적인 2개의 상태에 대한 확률을 나타내기 위해서는 1개의 수만 있으면 된다.
ex) 동전 앞이 나올 확률 p, 뒤가 나올 확률 1-p - Categorical distribution
n개의 분류가 나오는 상태에 대한 확률을 나타내기 위해서는 n-1개의 수가 있으면 된다.
마지막 분류에 대한 확률은 1-(다른 분류들에 대한 확률들의 합)을 해주면 알 수 있다
예를 들어 주사워의 각 면이 나올 확률을 나타내기 위해서는 1~5가 각각 나올 확률을 저장할 5개의 파라미터가 필요하고, 6이 나올 확률은 1-(1~5가 나올 확률을 더한 것)이 되므로 파라미터가 필요 없다 .그래서 총 5개가 필요하다.
RGB joint distribution
이미지에 대해서 생각해보자
이미지 한 pixel은 1개의 color로 이루어져있고 색은 RGB로 나타낸다.
RGB는 각각 256까지의 수로 나타내면 한 픽셀을 결정짓는데 256*256*256의 경우가 있을 수 있다.
한 pixel을 결정짓는 확률(하나의 픽셀을 fully describe하게 위해서 필요한 파라미터 수)은 256*256*256-1개의 파라미터가 필요하다.
Red에 대해서만 생각하면 간단하게 red1~256이 있다고 하면 해당 픽셀이 red1을 가질 확률에 대해서 1개의 파라미터가 필요하다. 각각 red2 red3에 대해서 가질 확률들도 각각 파라미터가 필요하기 때문에 red에 대해서만 256개가 된다. blue, green도 256개의 파라미터가 필요하고, 마지막 하나의 확률은 전체에서 빼면 되기 때문에 -1을 한다.
r,g,b는 각각 independent하다.
이미지에 대한 것은 256*256*256-1개 * 이미지전체 픽셀 수 만큼이 필요할 것이다.
Structure Through independence
각 픽셀이 검정 혹은 흰색으로만(binary) 표현되는 이미지가 있다

이 이미지가 가로10 세로10 = 100픽셀로 이루어져 있다고 하자.
Fully dependence
한 픽셀에 가능한 경우는 검정일 확률을 저장한 파라미터, 흰색일 확률을 저장한 파라미터 2개가 필요하다. 한 픽셀 안에서 검정일 확률을 1에서 빼면 1-(검정확률) 한 픽셀 안에서 흰색일 확률을 알 수 있다고 착각할 수 있지만, 그건 각 픽셀이 독립적일 경우이고 지금은 그렇지 않다. 그렇기 때문에 하나의 픽셀에 필요한 파라미터는 2개이다.
이러한 이미지가 나올 수 있는 경우의 수는 $2\times2\times \dotsb \times 2= 2^{n}$ 개이고 저 이미지는 $2^{n}$개 중의 한 경우일 것이다.
그럼 이 이미지가 될 확률을 표현하기 위한 파라미터 수는 $2^{n=100}-1$이 될 것이다.
$2^{n}$-1 개의 이미지가 각 이미지가 될 확률을 저장하고 있다고 생각하면 된다. 마지막 남은 하나는 1- ($2^{n}-1$개의 이미지가 될 확률을 모두 더한 것)으로 알 수 있기 때문이다.
Fully independence
하지만 이제 n개의 픽셀끼리 의존적이지 않고 독립적으로 생각해보자. 사실 말이 되지 않는다. 어떤 그림을 표현할 때 옆 픽셀의 영향을 받고, 이어질 가능성이 커지기 때문이다.
여전히 각 픽셀이 검정이거나 흰색이기 때문에 $2^{n}$개의 가능한 경우가 존재한다.
하지만 이 분포를 표현하기 위한 파라미터 수는 n개만 있으면 된다. 즉 이 이미지에 생성될 확률을 표현하는데 필요한 파라미터 수는 n개이다. 각 픽셀에 대해서 파라미터가 1개만 있으면 되기 때문이다. 각 픽셀이 독립적이 때문에 그 픽셀이 검정일 확률을 저장할 파라미터 1개만 필요하고 흰색일 확률은 1-(검정확률)을 하면 된다.
각 픽셀을 독립적이라고 여기기만 했는데 $2^{n}-1$에서 n개로 필요한 파라미터가 훅 줄었다. 하지만 표현할 수 있는 이미지가 적고 말이 안 되는 가정이다.
Conditional independence
그래서 fully independence와 fully dependence 사이의 어딘가를 찾아보자.
그러기 위해서는 3개의 rule이 필요하다.
Chain rule
$$p(x_{1}, \dotsb, x_{n}) = p(x_{1})p(x_{2}|x_{1})p(x_{3}| x_{1},x_{2}) \dotsb p(x_{3}| x_{n},\dotsb x_{n-1})$$
n개의 joint distribution을 n개의 conditional distribution으로 바꾼다.
independent이든 아니든 상관없이 만족한다.
Bayes' rule
$$p(x|y)=\frac{p(x,y)}{p(y)} = \frac{p(y|x)p(x)}{p(y)}$$
이 또한 independent이든 아니든 상관없이 만족한다.(=exact하다)
Conditional independence
x,y,z는 모두 random variable 이다.
z가 주어졌을 때, x와 y가 independent하다는 가정아래
$$p(x|y,z) = p(x|z)$$
뒤의 condition을 날려주는 효과가 있다
chain rule을 사용해도 여전히 분포를 표현하기 위해서 필요한 파라미터 수는 변하지 않는다.
$p(x_{1})$ : 1개의 파라미터가 필요
$p(x_{2}|x_{1})$ : $p(x_{2}|x_{1})=0$을 표현할 파라미터, $p(x_{2}|x_{1})=1$을 표현할 파라미터, 총 2개의 파라미터가 필요
$p(x_{3}|x_{1}, p(x_{2})$ : $p(x_{3}|x_{1}) =0$, $p(x_{3}|x_{1}) =1$, $p(x_{3}|x_{2}) =0$, $p(x_{3}|x_{2}) =1$, 총 4개의 파라미터가 필요
결국 $1+2+2^{2}+ \dotsb + 2^{n-1} = 2^{n}-1$ 개의 파라미터가 필요해서 전과 똑같은 수의 파라미터가 필요하다.
그래서 markov assumption을 추가한다.
예를들어 10번째 픽셀은 9번째 픽셀에만 의존적(dependent)하고, 1~8번째 픽셀에는 independent한 것이다.
markov assumption을 적용하면 아까의 chain rule 식이
$$p(x_{1}, \dotsb, x_{n}) = p(x_{1})p(x_{2}|x_{1})p(x_{3}| x_{2}) \dotsb p(x_{n}| x_{n-1})$$
이렇게 간략하게 된다.
이렇게 되면 $2n-1$개의 파라미터만 필요하게 된다. 첫번째 $p(x_{1})$에만 1개의 파라미터가 필요하고 나머지 $p(x_{2}|x_{1})$는 $p(x_{2}|x_{1})=0$과 $p(x_{2}|x_{1})=1$에 대한 것 2개의 파라미터가 필요하게 되기 때문이다.
fully dependent와 비교했을 때 지수적으로 수가 줄어들었다. ($2^{n}-1 \rightarrow 2n-1$)
Auto-regressive Model
이렇게 conditional independency를 잘 활용한 모델을 auto-regressive model이라고 한다.
joint distribution을 chain model로 쪼개서 conditional distribution 바꾸는데,
파라미터 수뿐만 아니라, NN이나 모델에 적용하려면 어떻게 적용할 수 있을까
auto regressive model은 하나의 정보가 이전 정보들에 dependent하다는 것을 가정한다.
markov assumption처럼 i번째 픽셀이 i-1에만 dependent하는 것도 물론 되고,
i번째 픽셀이 1~i-1픽셀까지 모든 픽셀에 dependent한 것도 된다.
픽셀들을 어떻게 순서를 매길지도 중요하다.

이미지는 2차원인데 순서는 1차원이기 때문에 순서를 매기는 방법에 따라 성능이나 방법론이 달라질 수 있다.
또한 auto regressive가 이전 3개만 고려할 수도 있고 5개만 고려할 수도 있다. 그 수에 따라
ar3 model, ar5 model 등으로 부른다.
이렇게 어떤식으로 conditional indepency를 주느냐에 따라서 전체 모델의 structure가 달라지게 된다.
NADE : Nerual Autoregressive Density Estimator

i번째 픽셀을 1 ~ i-1번째 픽셀에 dependent하게 하게 한다.
| 1 번째 픽셀에 대한 확률 분포 | 2 번째 픽셀에 대한 확률 분포 | 5 번째 픽셀에 대한 확률 분포 | i 번째 픽셀에 대한 확률 분포 |
| 어느 픽셀에도 depedent 하지 않게 독립적으로 만듦 | 1 번째 픽셀에만 dependent (=1 번째 픽셀 값을 입력으로 받는 neural network를 만들어서 scalar를 sigmoid를 거쳐서 확률이 되도록 함) |
1,2,3,4 픽셀에 대해 dependent | 1 ~ i-1번째 픽셀에 대해 dependent |
| 1 | 4 | i-1 |
neural network입장에서는 입력값이 계속 커지고 weight도 계속 커진다.
이렇게 binary입력일 때는 sigmoid를 사용하지만, 연속적인 값이 입력일 때는, gaussian model를 마지막 layer에 활용한다.
NADE는 explicit model이다. 단순히 generation만 할 수 있는 것이 아니라 입력 vector가 주어지면 확률을 계산할 수 있다.
n개의 픽셀($x_{1},x_{2},x_{3}, \dotsb x_{n}$)이 입력으로 들어가면
$$p(x_{1}, \dotsb, x_{n}) = p(x_{1})p(x_{2}|x_{1})p(x_{3}| x_{2}) \dotsb p(x_{n}| x_{n-1})$$
을 계산할 수 있게 되면서 작지만 확률을 구할 수 있다.
그래서 density모델이고 density가 이름에 들어가 있으면 explicit model일 확률이 높다.
Pixel RNN
이미지에 대한 pixel을 만들어내는 generative model.
$n\times n$ RGB이미지에 대해서 순차적으로 R, G, B를 만든다.
$$p(x) = \prod^{n^{2}}_{i=1} p(x_{i,R}|x_{<i}) p(x_{i,G}|x_{<i},x_{i,R} ) p(x_{i,B}|x_{<i}, x_{i,R}, x_{i,G})$$
NADE는 fully connected모델이었지만, RNN을 사용한다.
Ordering을 어떻게 하느냐에 따라서 2가지로 나뉜다.
- Row LSTM
위쪽의 정보 활용
- Diagonal BiLSTM
자기 전 모든 정보 활용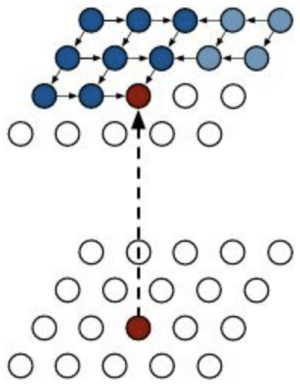
'부스트캠프 AI Tech 3기 > 이론 : U-stage' 카테고리의 다른 글
| [Day17] AI 서비스 개발 2. 머신러닝 프로젝트 라이프 사이클 (0) | 2022.02.14 |
|---|---|
| [Day16] DL Basic 10. Generative Model - 2 : VAE, GAN (0) | 2022.02.12 |
| [Day15] DL Basic 8. Sequential Models - Transformer (0) | 2022.02.10 |
| [Day15] DL Basic 7. Sequential Models - RNN (0) | 2022.02.09 |
| [Day14] DL Basic 6. Computer Vision Applications : Semantic Segmentation, Detection (0) | 2022.02.09 |


