Convolution
신호 처리에서 두 함수 f와 g를 섞어주는 것으로 나타난다.
- Continuous convolution
$$(f*g)(t) = \int f(\tau)g(t-\tau)d\tau=\int f(t-\tau)g(t)d\tau$$ - Discrete convolution
$$(f*g)(t)=\displaystyle\sum^{\infty}_{i=-\infty} f(i)g(t-i)=\displaystyle\sum_{i=-\infty}^{\infty}f(t-i)g(i)$$ - 2D image convolution
$$(I*K)(i,j)=\displaystyle\sum_{m}\displaystyle\sum_{n}I(m,n)K(i-m, j-n)=\displaystyle\sum_{m}\displaystyle\sum_{n}I(i-m,j-n)K(m, n)$$
$I$가 전체 이미지 공간, $K$는 적용하고자 하는 convolution filter가 된다.
2D convolution
연산법
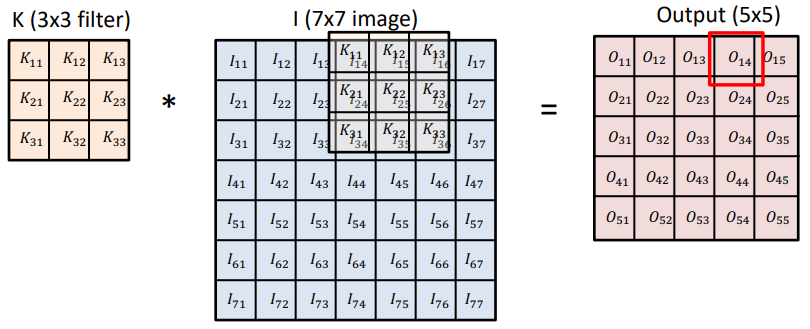
사진에서 $K_{11}$와 $I_{11}$같은 사각형 안에는 수가 들어가게 된다. $I_{11}$는 이미지 한 부분을 이루는 한 픽셀이다.
k의 필터를 이미지 위에서 하나하나 곱해가며 output을 만들어 나간다.
예시로 $o_{11}=K_{11}I_{11}+K_{12}I_{12}+K_{13}I_{13}+K_{21}I_{21}+ \dotsb$와 같이 9개의 k와 I까리 성분곱을 하면 된다.
filter의 크기가 있기 때문에 원래 이미지보다 output이미지가 줄어들게 된다.
해당 convolution filter(=kernel)의 모양을 해당 이미지에 찍는 것이다.
Stride
filter를 몇 칸씩 옮겨가며 계산할지
stride가 작을수록 convoluion filter를 dense하게 찍게 된다.
2D에서는 방향이 2개이기 때문에 stride가 width와 height 두 방향으로 2개가 필요하다. 하지만 2D에서도 stride가 1개만 표시되어 있으면 width와 height의 stride가 같은 것이다.
Padding
image의 가장자리에 특정한 수로 테두리를 둘러주는 것이다.
어떤 값이 채워져 있어야 convolution filter가 삐져나오지 않고 모두 찍을 수 있기 때문이다.
zero padding이라고 하면 모두 0 으로 채워지는 것이다.
3D convolution

5X5 필터를 convolution한다고 하면 image와 같은 channel만큼의 channel수를 가지고 있어서 5X5X3이라는 뜻이 내포되어 있다.
여기서 주목해야할 것은 output의 channel이 1이 되었다는 것이다.
그래서 output channel이 x개라면 filter의 수(filter의 channel이 아니다)도 x개 된다.
즉, input channel와 output channel의 수를 알면 filter의 수를 알 수 있다.

4 5x5x3
에서 4는 output channel수로, 3은 input channel수 맞춰주면 된다는 것을 알 수 있다.
또한, 이 연산을 정의하는데 필요한 파라미터의 숫자를 잘 보아야 한다. 얼마나 파라미터가 필요한지에 대한 감이 있어야 한다. 왜냐하면 파라미터수는 generalization performace와 관련이 있기 때문이다. 그래서 네트워크 구조를 보면서 대충 몇 만개, 몇 십만개의 파라미터가 필요하겠다는 단위에 대한 감을 잡아보는 것이 좋다.
CNN : Convolutional Neural Networks
위의 convolution을 사용한 layer를 포함해서 cnn이라고 한다.
CNN은
- Convolution layer
feature를 추출한다. - Pooling layer
feature를 추출한다.
ex)max pooling - Fully connected layer
분류나 회귀에서 원하는 출력값을 결정한다.
fully connected는 input layer의 파라미터(neural net)의 갯수의 output layer의 파라미터 갯수를 곱한 것만큼의 파라미터가 필요하기 때문에 convolution layer와는 비교가 안 되게 많은 파라미터가 필요하다.
최근들어서 fully connected layer를 최소화 시키고 있다. 왜냐하면 parameter수가 늘어날 수록 학습이 어렵고 generalization performance가 떨어지기 때문이다.
로 이루어져 있다.
CNN을 깊게 쌓지만 파라미터 숫자는 줄이는 방향으로 발전한다.
1x1 Convolution
이미지의 영역이 아니라 한 픽셀만 본다. 그러면 왜 하는 것일까?
- Dimension(channel) reduction
이미지 크기는 유지한채로 channel 수만 줄이기 위해서 - depth는 깊게 하면서 파라미터수는 줄이기 위해서
bottleneck architecture에서 사용된다.
'부스트캠프 AI Tech 3기 > 이론 : U-stage' 카테고리의 다른 글
| [Day14] DL Basic 6. Computer Vision Applications : Semantic Segmentation, Detection (0) | 2022.02.09 |
|---|---|
| [Day14] DL Basic 5. Modern CNN (0) | 2022.02.09 |
| [Day13] DL Basic 3. Optimization - 3 : Regularization (0) | 2022.02.08 |
| [Day13] DL Basic 3. Optimization -2 : Optimizers (0) | 2022.02.08 |
| [Day13] DL Basic 3. Optimization 최적화 - 1 (0) | 2022.02.08 |


