1. Generalization
대부분 일반화 성능을 높히는 것이 목적이다.
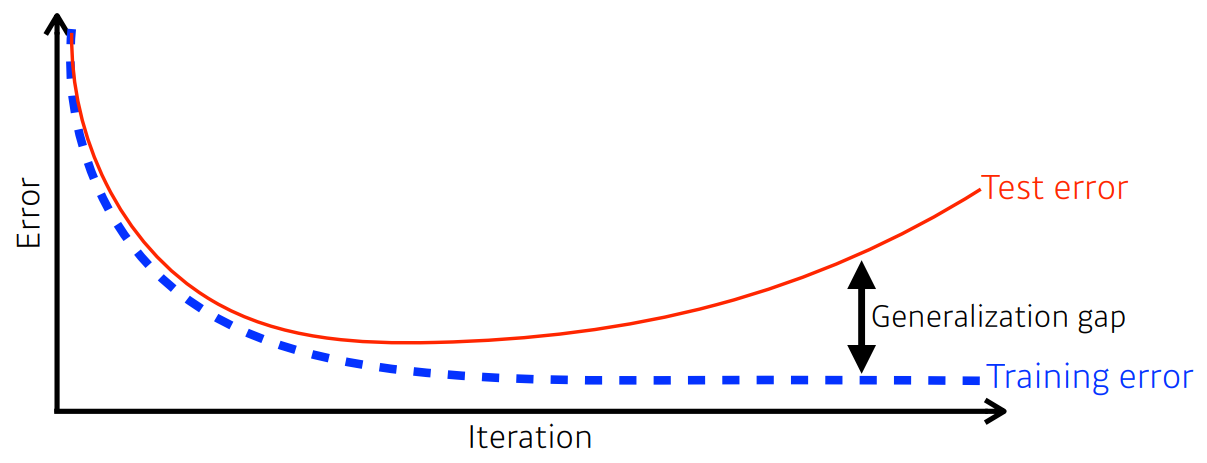
training error가 낮아져도 학습이 잘 됬다는 보장은 없다. test error에 대해서는 커질 수 있다.
그래서 training error와 test error 사이의 차이를 generalization gap이라고 하고,
generalization 성능이 좋다는 것은 이 network의 성능이 학습 데이터의 성능과 비슷할 것이라는 의미이다.
2. Underfitting vs Overfitting
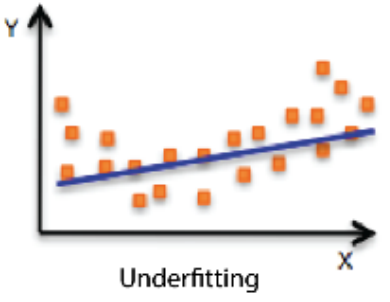
| Underfitting | Balanced | Overfitting 과적합 |
 |
 |
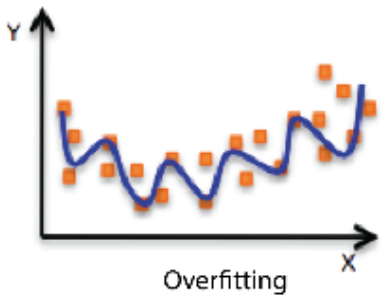 |
| training을 너무 적게 해서 학습 데이터 조차도 잘 못 맞추는 현상 | 그 사이 좋은 network | 학습 데이터에 대해서는 잘 동작하지만 test 데이터에 대해서는 잘 동작하지 앟는 현상 |
3. Cross validation
주어진 학습데이터에서 한 번 더 나누어서 validation을 위한 dataset을 만든다.
그래서 학습에 사용되지 않은 validation data를 기준으로 성능을 평가한다.
대표적으로 k-fold가 있다.
학습데이터를 k개로 나눈 후 k-1개의 데이터 덩어리로 학습시키고 1개의 덩어리로 validation을 한다.
이 과정을 k번 반복해서 나온 k개의 성능을 평균내서 최종 성능으로 생각한다.
cross validation을 통해 hyper parameter을 정한 후 모든 학습 데이터에 대해서 학습시킨다.
※parameter : 최적화해서 찾고 싶은 값
※hyper parameter : 내가 정하는 값
4. Bias-variance

variance은 출력이 일관적으로 나오느냐와 관련이 있다.
variance가 낮으면 일관적이다.
variance가 높아지면 출력이 일관적이지 못해서 overfitting될 가능성이 높아진다.
평균적으로 봤을 때 출력이 분산이 커지더라도 target에 접근하면 bias는 낮다.
bias가 높으면 mean과 많이 벗어나게 된다.
Bias and Variance trade off theorem
학습 데이터에 노이즈가 있다고 가정했을 때, 이 학습 데이터에 대한 network의 cost를 minimize하는 것은 세 가지 요소로 이루어져 있다.
- bias
- variance
- noise
그래서 각각을 줄이는 것이 cost를 줄이는 것이 아니라 하나를 줄이면 하나는 커질 수 밖에 없다.
$$ \mathbb{E} [(t-\hat{f})^{2}]= \mathbb{E}[(t-f+f-\hat{f})^{2}]$$
$$=\mathbb{E}[(f-\mathbb{E}[\hat{f}]^{2})^{2}] + \mathbb{E}[ ( \mathbb{E} [\hat{f}]-\hat{f} )^{2} ]+\mathbb{E}[\epsilon]$$
cost = bias ($\mathbb{E}[(f-\mathbb{E}[\hat{f}]^{2})^{2}]$) + variance ($\mathbb{E}[ ( \mathbb{E} [\hat{f}]-\hat{f} )^{2} ]$) + noise ($\mathbb{E}[\epsilon]$)
cost를 minimize하는 것은 bias와 variance와 noise를 minimize하는 것으로 구성되어 있다.
$t$ : target
$\hat{f}$ : neural network의 출력값
그래서 noise가 있으면 사실 bias와 variance를 둘 다 줄이기는 어렵다.
5. Bootstrapping
데이터 중에 random으로 여러 개를 sampling해서 각각을 모델로 만든다.
각 모델이 예측한 값들이 일치를 이루는 지 보고, 전체적인 모델의 uncertainty를 예측하고자 할 때 bootstrapping을 사용한다.
6. Bagging and boosting

Bagging
Bootstrapping aggregating
학습 데이터를 일부만 사용해서 여러 모델을 만들고 그 모델들의 output의 평균을 내는 방식
앙상블이 bagging에 속한다.
Boosting
예측하기 어려웠던 데이터들에 대해서만 따로 모델(weak learner)을 만들어 모든 모델 연속적(sequential)으로 합쳐서 하나의 큰 모델(strong learner)을 만드는 방식
Gradient Descent Methods
- Stochastic gradient descent : SGD
1개의 sample만 사용해서 update (엄밀하게 따졌을 때)
random하게 sampling - Mini-batch gradient descent
전체 data를 다 사용하지는 않지만 SGD처럼 1개만 사용하는 것도 아니다.
예를 들어 100개의 데이터를 batch size=20이라면 5개의 batch가 생기고,
update할 때마다 batch 하나를 가져와서 사용한다
최근에는 batch gradient라고 하면 mini batch gradient descent를 가리키는 경우가 많다고 하는데 나는 이 때 mini batch gradient descent가 가리키는게 MSGD가 아니라 mini batch gradient descent일 것이라고 생각한다. (개인적으로..) - Mini-batch Stochastic gradient descent : MSGD
전체 data 중에서 random하게 batch size만큼 sampling해서 사용
random sampling 에 대한 내용은 https://classic.d2l.ai/chapter_optimization/minibatch-sgd.html 를 참고했다.
위의 Mini-batch gradient descent와 다른 점은 random sampling 밖에 없다.
최근에는 MSGD를 SGD라고 표현된다. - Batch gradient descent
한 번에 모든 데이터를 다 사용한다.
모든 gradient의 평균을 가지고 update한다.
왜 MSGD를 MSGD로 부르지 않고 SGD로 부르고, 왜 batch도 mini batch를 가리키는지에 대한 이유는 실제로 1개의 sample만 사용하는 경우는 거의 없고, 전체를 다 사용하는 경우도 거의 없기 때문인 것 같다. 그냥 mini batch가 국룰이라 뭘 말하든 다 mini batch를 뜻하게 되는 것 같다.

개인적인 생각으로 정리한 부분이 포함되어 있습니다,, 틀린게 있다면 말씀해주세요
Batch-size
batch size를 크게 ex 512, 1024.. 쓰면 sharp minimizer에 도달한다.
작게 쓰면 flat minimizer에 수렴한다.
실험적으로 batch size를 작게 쓰는 것이 좋다.
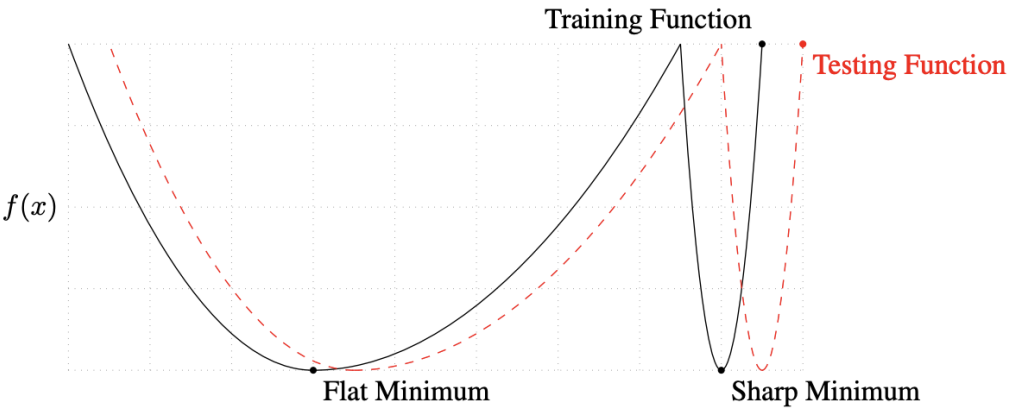
testing function의 minimum을 찾는 것이 목적인데,
flat minimum에서는 testing function과 조금 떨어져도 flat하게 때문에 성능차이가 크게 나지 않는다.
다른말로 generalization 성능이 높은 것이다.
하지만 sharp minimum은 조금만 떨어져도 성능차이가 커져버린다.
'부스트캠프 AI Tech 3기 > 이론 : U-stage' 카테고리의 다른 글
| [Day13] DL Basic 3. Optimization - 3 : Regularization (0) | 2022.02.08 |
|---|---|
| [Day13] DL Basic 3. Optimization -2 : Optimizers (0) | 2022.02.08 |
| [Day13] DL Basic 2. 뉴럴 네트워크 - MLP (0) | 2022.02.07 |
| [Day12] Data Viz 4-1. Seaborn 소개 (0) | 2022.02.07 |
| [Day12] Data Viz 3-4. More Tips (0) | 2022.02.07 |

