[Day35] RecSys with DL 7-1 RecSys with GNN

Graph

Node(꼭짓점)과 그 Node들을 잇는 Edge로 이루어진 자료구조

데이터들이 서로 연결되어 있을 때 표현하기 적합니다.

$$G =(V,E)$$

ex) $G=({A,B,C}, {{A,B},{C,A}})$

• $V$
  Node들의 집합
  → {A,B,C}
• $E$
  Edge들의 집합
  →{{A,B},{C,A}}

Graph를 사용하는 이유

1. 객체 사이의 관계나 상호작용같은 추상적인 개념을 테이블같은 정형화된 구조보다 다루기 적합하다.
   ex) 소셜 네트워크, 바이러스 확산
   유저-아이템 소비 관계도 유저, 아이템을 노드로 두고 유저가 아이템을 사용하면 두 노드를 엣지로 이으면 표현할 수 있다.
2. Non-Euclidean Space의 표현 및 학습이 가능하다
   우리가 흔히 다루는 이미지, 엑셀과는 다른 데이터를 사용한다. 이런 데이터들은 격차 형태로 표현할 수 있다고 표현하는데, 이 표현은 Euclidean space에 표현할 수 있다는 말과 같다. Euclidean space는 익숙하게 다루는 2,3차원 공간을 일반화시킨 것이다. 또한 실수로 표현되어 있다.
   
   하지만 실수로 표현할 수 없는 데이터는 그래프를 사용하지 않으면 더 복잡하게 표현되어, 그래프로 표현을 단순하게 만들 수 있다.

 

Graph Neural Network : GNN

그래프를 신경망에 적용한 것

노드에 연결된 이웃 노드들의 정보를 GNN이 표현할 수 있어야 한다. 그래서 그래프를 표현할 수 있는 인접행렬을 만들어서 인접행렬을 GNN의 input으로 사용할 수 있다. 

두 노드가 연결되어 있으면 해당하는 행렬을 1로 표시해서 인접행렬을 채우고, 원래 가지고 있던 feature를 같이 넣어준다. 

 

하지만, 노드가 증가하면 인접행렬의 차원이 늘어나고 GNN도 늘어난다. 그럼 모델의 연산량은 점점 많아지면서 입력데이터는 sparse해진다. 또한, 인접행렬은 지금은 ABC순서로 되어 있지만 조금 순서가 바뀌면 의미가 달라질 수 있다. 그래서 노드가 많아질수록 기하급수적으로 연산량이 늘어나서 이런 naive approach는 한계가 극명하다.

 

A Comprehensive Survey on Graph Neural Networks

GCN(Graph Convolution Network)은 이런 단점을 보완한다. 이미지에서 filter로 convolution을 시키듯이 graph으로 확장시켜 적용한다. 주어진 데이터와 가까이 있는 데이터에 convolution하는데, graph에서는 하나의 엣지로만 연결되어 있는 이웃들을 convolution 연산한다.

 

Image convolution과 Graph convolution의 공통점

• local connectivity
  이미지의 convolution과 graph의 convolution이 근처에 있는 노드(데이터)에 convolution 연산을 수행한다는 같은 원리 사용한다
• shared weight
  CNN에서 convolution 연산을 할 때 filter를 사용하는데, filter라는 weight를 정해두고 계속해서 같은 값을 옆으로 옮겨가며 사용한다. graph convolution에서도 어느 노드가 중심이 되는 같은 파라미터를 share한다.
• multi-layer
  여러 layer를 쌓으면 바로 옆의 데이터 외에 더 멀리 있는 데이터까지 참고할 수 있다. Graph에서도 하나 더 옆의 이웃노드까지 참고할 수 있다.

그래서 graph convolution을 하면 연산량을 줄이면서 깊은 네트워크로 멀리있는 관계의 특징까지 추출/참고할 수 있다. 그래서 보통 GNN이라고 하면 GCN을 사용한 모델이다.

 

Neural Graph Collaborative Filtering

: GNN을 기반으로 유저-아이템의 상호작용(collaborative signal)을 추출하는 모델

: graph의 장점을 이용해서 임베딩 레이어에서 collaborative signal을 직접 추출한다.

 

기본적인 Collaborative Filtering(ex. MF)같은 모델은

• 유저와 아이템의 임베딩
  one-hot encoding으로 표현된 임베딩을 dense하게 바꾼 latent vector
• 유저와 아이템의 상호작용 모델링
  임베딩 이후 내적해서 유저와 아이템의 상호작용을 linear하게 표현하는 방법이 대표적이다.

을 잘 학습해야 한다는 것을 알 수 있다.

 

하지만 NGCF이전에는 유저와 아이템의 상호작용을 임베딩 단계에서 접근하지 못하고 분리되어 있다. Neural CF도 임베딩을 concatenate를 하기 때문에 임베딩과 분리되어 있다.

 

Collaborative signal

GNN은 유저와 아이템의 상호작용이 임베딩할 때부터 반영될 수 있도록 한다.

Neural Graph Collaborative Filtering

user-time interaction graph에서는 $u_1$은 $i_4$와는 연결되어 있지 않아서 유저,아이템 갯수가 많아질수록 상호작용을 놓치지 쉽다.

 

High-order Connectivity는 경로가 1보다 큰 연결이라는 뜻이다. High-order Connectivity에서는 같은 상호작용을 length가 3인 그래프로 확장된다. $u_1,u_2$는 $i_2$를 가지고 상호작용하기 때문에 서로 유사하다고 말할 수 있다. 또한, $i_4, i_5$가 그래프를 타고 올라가서 $u_1$에게 추천될 가능성이 높다는 것도 알 수 있다. 또한 $i_3$쪽에도 $i_4$가 있기 때문에 $i_4$가 $i_5$보다 추천될 가능성이 높다. 하나의 노드를 기준으로 high-order connectivity를 이용해서 한 유저에 대한 다양한 표현을 GNN은 할 수 있다.

 

구조

위 사진에서 오른쪽은 user에 대해서, 왼쪽은 item에 대해서 임베딩을 구하는 것이다.

Embedding layer : 임베딩 레이어

처음 입력된 one-hot encoding을 k차원의 임베딩으로 바꾼다.
$$E=[e_{u_{1}},\dotsb, e_{u_{N}},\;e_{i_{1}}, \dotsb, e_{i_{M}}]$$
임베딩을 이전까지는 바로 interaction function에 입력되어서 바로 선호도를 예측했었지만,
NGCF에서는 GNN상으로 전파시켜서 GNN 상에서 refine되도록 한다. collaborative signal을 명시적으로 임베딩 레이어에 주입하기 위해서이다. 임베딩 레이어에서는 결과적으로 임베딩을 만들기만 한다.

 

Embedding propagation layer : 임베딩 전파 레이어

1번에서 생성된 임베딩 레이어를 전파시켜 high-order connecvity가 학습된다. message에 유저-아이템의 collaborative signal을 담아서 표현한다.

 

Message construction

$$m_{u\leftarrow i}=\frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}\left(W_1e_i+W_2(e_i\odot e_u)\right)$$

• m_{u\leftarrow i}
  아이템 i에서 u로 전달되는 메세지
• $W_{1}e_{i}$
  아이템 자체가 가진 임베딩
• $e_i\odot e_u)$
  아이템 i 와  유저u의 상호작용
• $\frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}$
  정규화 term
• $\mathcal{N}_i, \mathcal{N}_u$
  유저, 아이템의 이웃한 유저, 아이템 집합
• $|\mathcal{N}_i|, |\mathcal{N}_u|$
  이웃한 노드의 갯수
• $W_1,W_2$
  weight matrix
• $\odot$
  element-wise production

 

위의 수식은 유저노드 기준으로 적힌 식이다.

이런 message가 유저마다 1개가 아니라 여러 아이템에 대해 존재할 것이다.

 

Message Aggregation

그래서 최종적으로 유저임베딩을 구하는 과정은

$$e_u^{(1)}=\text{LeakyReLU}\left(m_{u\leftarrow u}+\sum_{i \in \mathcal{N}_u}m_{u\leftarrow i} \right)$$

• $e_u^{(1)}$
  첫 번째 레이어의 최종 유저 임베딩
  1-hop까지 전파된 임베딩
• $\sum_{i \in \mathcal{N}_u}m_{u\leftarrow i}$
  아이템  i에서 u로 전달되는 메세지를 모든 인접 노드들에 대해서 더한 것

 

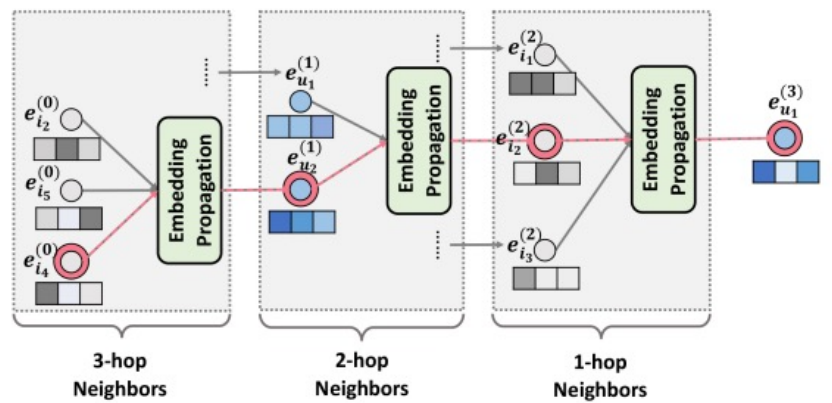
path를 여러 개 쌓아서 l개까지 쌓을 수 있고 l-차 이웃까지도 임베딩 전파가 이루어진다.

※l-차 이웃 : path가 l개만큼 떨어져 있는 이웃

 

3단계의 임베딩을 구하기 위해서는 2단계의 임베딩을 구해야만 하기 때문에 이 관계를 점화식으로 표현할 수 있다.

 

High-order Propagation

$$\begin{aligned}
m_{u\leftarrow i}^{(l)}&=p_{ui}\left( W_1^{(l)}e_i^{(l-1)}+W_2^{(l)}(e_i^{(l-1)}\odot e_u^{(l-1)})\right)\\m_{u\leftarrow u}^{(l)}&=W_1^{(l)}e_u^{(l-1)}
\end{aligned}​$$

 

$e^{l-1}$로부터 $e^{l}$을 만드는 과정인데, 수식은 위에서 1차로 보았던 것과 같은 개념이지만 점화식으로 일반화한 것이다. 위의 두 식에 의해 정리된 $m_{u\leftarrow i}^{(l)}$과 $m_{u\leftarrow u}^{(l)}$를

 

$$e_u^{(l)}=\text{LeakyReLU}\left(m_{u\leftarrow u}^{(l)}+\sum_{i \in \mathcal{N}_u}m_{u\leftarrow i}^{(l)} \right)$$

에 대입한다.

 

이렇게 embedding을 여러개 쌓는 것, path를 여러 개의 정보를 현재 노드를 기준으로 전달하는 과정을 high-order propagation이라고 한다.

Prediction layer : 유저-아이템 선호도 예측 레이어

임베딩 전파 레이어의 output들이 concatenate되어 prediction layer에서 예측하게 된다.

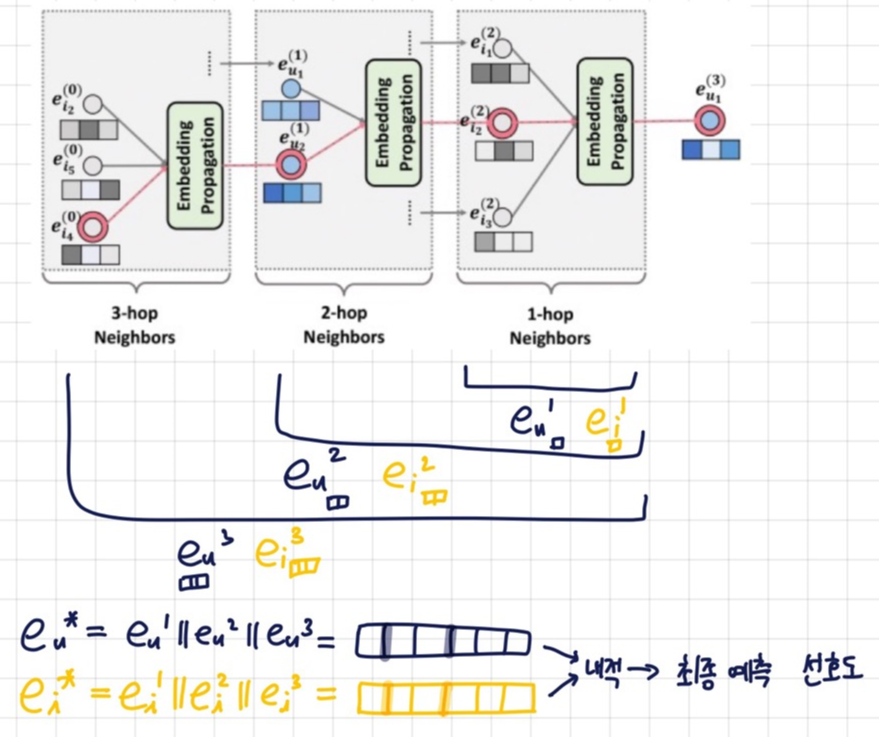
L개의 전파 레이어(L-차의 임베딩 벡터)를 사용했다고 하면 $e_{u}^{(0)}$부터 $e_{u}^{(L)}$까지 l+1개의 유저 임베딩과 l+1개의 아이템 임베딩이 생성될 것이다.

 

$$e_u^*=e_u^{(0)}\Vert\cdots\Vert e_u^{(L)} \qquad e_i^*=e_i^{(0)}\Vert\cdots\Vert e_i^{(L)}$$

||기호는 concatenate하는 것이다.

 

유저임베딩에 대해서 하나, 아이템 임베딩에 대해서 하나 이렇게 만들어 진 것을 내적해서 최종 선호도 예측값을 계산한다.

$$\hat{y}_{NGCF}(u,i)=e_u^{*T}e_i^*$$

 

결과 및 요약

임베딩 전파 레이어가 많아질수록 모델의 추천이 높아지지만 너무 많으면 overfitting이 발생해서 l-3,4가 적당하다. 또한, MF보다 빠르게 수렴하고 recall 또한 높다. 왜냐하면 임베딩 전파를 통해 representation power가 좋아져 유저와 아이템을 더 잘 표현하게 되었기 때문이다.

 

LightGCN

GCN의 핵심 부분을 사용해서 정확하고 파라미터수는 적게 만든 모델

• Light Graph Convolution
  NGCF에서는 임베딩 전파에서 convolution할 때, 파라미터를 곱하고 leaky ReLU를 사용한다.
  하지만 lightGCN은 임베딩을 가중합 하기만 한다.
  →적은 파라미터와 연산량
• Layer combination
  임베딩 전파 레이어의 깊이가 깊어질수록 강도가 약해질 것이라고 가정해서 임베딩을 합칠 때도 모델을 단순하게 했다.

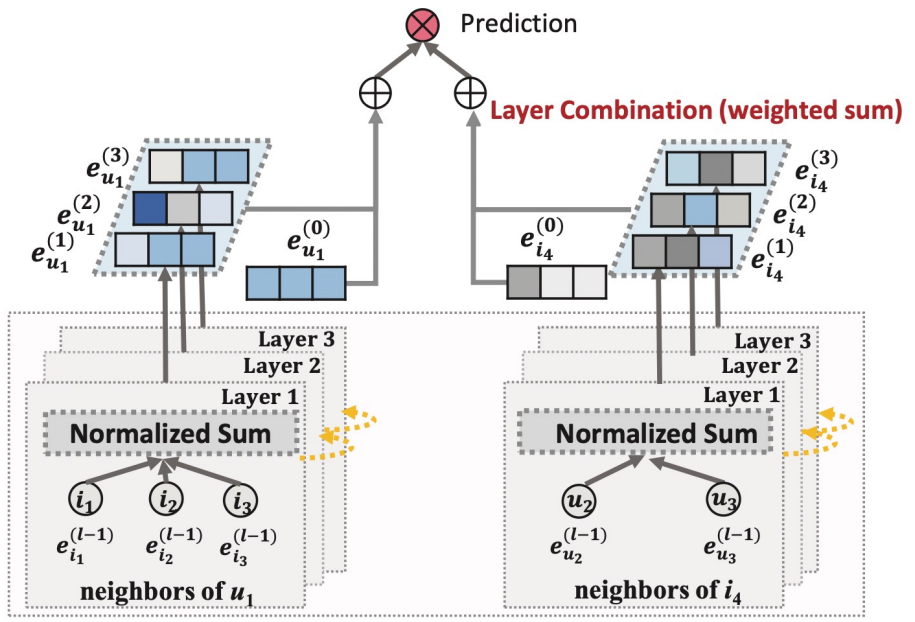
임베딩 전파 레이어

전 차수의 임베딩에 학습 파라미터를 곱하고 activation function 까지 적용해야하는 NGCF에 비해

 

LightGCN은 전 차수의 임베딩을 가중합하는 것이 전부이다. 그래서 user에서 user로 가는 self connection도 없고, user에서 item으로 가는 임베딩만 사용한다. 또한 학습 파라미터도 0번째 layer에서 one-hot encoding을 임베딩으로 표현할 때만 사용한다.

 

$$e_u^{(k+1)}=\sum_{i\in \mathcal{N}_u}\frac{1}{\sqrt{|\mathcal{N}_u|}\sqrt{|\mathcal{N}_i|}}e_i^{(k)}\\
e_i^{(k+1)}=\sum_{u\in \mathcal{N}_i}\frac{1}{\sqrt{|\mathcal{N}_i|}\sqrt{|\mathcal{N}_u|}}e_u^{(k)}$$

 

유저-아이템 선호도 예측 레이어

NGCF는 모든 차수의 임베딩을 concatenate하는데, LightGCN은 $\alpha_{k}$를 이용해서 단순하게 더한다.

그래서 차원이 늘어나는 것도 방지하고 압축해서 표현할 수 있다.

 

$$e_u=\sum_{k=0}^K \alpha_ke_u^{(k)}$$

$$e_i=\sum_{k=0}^K \alpha_ke_i^{(k)}$$

 

$\alpha_{k}$를 하이퍼 파라미터로 하거나, 학습 파라미터로 하거나 둘 다 상관없다고 한다. 차이가 크지 않다.

$$\alpha_k=\frac{1}{k+1}$$

위와 같은 식으로 하이퍼 파라미터로 두면 레이어가 깊어질수록 가중치는 낮아지게 하는 역할을 한다. 임베딩이 전파질수록 signal이 약해진다는 아이디어를 적용한 것이다.

 

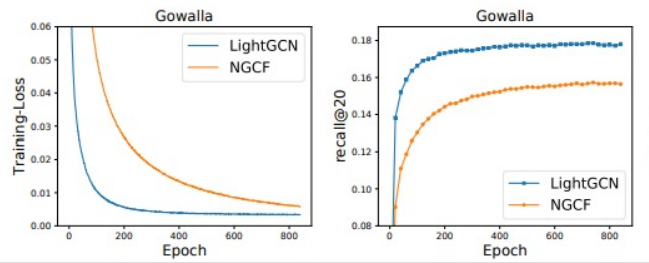
결과 및 요약

recall, loss 모두 NGCF보다 뛰어난 것을 확인할 수 있다. 이는 NGCF보다 LightGCN이 generalization이 잘 된다는 뜻이다. 현업에서도 많이 사용하고 있는 모델이라고 한다.