Bayesian Personalized Ranking : BPR
implicit feedback를 사용해 MF를 학습할 수 있다.
베이지안 추론에 기반해서 implicit data로 서로 다른 아이템에 대한 유저의 선호도를 반영한다.
Personalized Ranking
사용자에게 ranking이 있는 아이템 리스트를 제공하는 문제 (=아이템 추천 문제)
유저가 아이템 i보다 아이템 j를 좋아한다는 정보를 이용해서 MF의 파라미터를 학습한다.
이 정보가 해당 유저의 personalized ranking이다.
사용자의 클릭이나 로그는 implicit data이기 때문에 선호도가 분명하게 드러나지 않다.
상호작용하지 않은 아이템에 대한 것은 관측데이터가 없어서 밑의 두 가지로 고려할 수 있다
- 유저가 아이템에 관심이 없다
- 유저가 아직 아이템을 모른다
그래서 유저의 아이템에 대한 선호도 랭킹을 생성해서 MF의 학습 데이터로 사용한다.
접근
- 관측된 item을 관측되지 않은 item보다 선호
- 관측된 아이템끼리는 누가 더 선호한다고 말할 수 없기 때문에 선호도를 추론하지 않는다.
- 관측되지 않은 아이템끼리 선호도를 추론하지 않는다.

유저-아이템 행렬을 유저별로 선호도 정보를 생성한다.
유저 $u_1$은 2,3은 선호하지만 1,4아이템에 대해서는 관측된 것이 없다. 유저 $u_1$의 행렬은 위의 사진에서 오른쪽 위의 행렬이다.
선호도를 비교할 수 있는 것은 + > ? 뿐이고 +와 +, ?와 ?는 선호도를 비교할 수 없다. 그러면 관측하지 않았던 ?에 대해서도 +와 비교당하면서 정보가 부여되었다! 그래서 관측하지 않았던 아이템들에 대해서도 ranking을 할 수 있다.
학습 데이터 생성
학습데이터 $D_s$
$$D_s:= \{(u,i,j)|i\in I_u^+ \wedge j\in I \backslash I_u^+ \}$$
- $l_u^+$ : 유저 u가 선호하는 아이템 집합
- $l\backslash l_u^+$ : (전체 아이템 집합) 차집합 (유저 u가 선호하는 아이템 집합) = 유저 u가 선호하지 않는 집합= 관측되지 않은 아이템 집합
유저 한명에 대해서 선호하는 아이템 i와 관측하지 않은 아이템j로 이루어진 집합으로 학습데이터를 만드는데, 이 집합을 triples 집합이라고 부른다.
위의 예시에서 유저 $u_1$의 선호도 데이터에서만 보면 4개의 유의미한 데이터가 학습데이터에 들어간다
$$i_2>_{u1}i_1,\quad i_3>_{u1}i_1, \quad i_2>_{u1}i_4,\quad i_3>_{u1}i_4$$
최대 사후 확률 추정 : Maximum A Posterior : MAP
이제 학습데이터로 파라미터 학습을 수행한다. 크게 MLE와 MAP가 있다. 그중 MAP를 살펴보자.
MAP는 베이지안 개념이 사용된다. 사후확률이 최대확률이 되는 파라미터를 찾는 것이다.
사후확률을 바로 구할 수 없기 때문에 bayesian 정리로 선회해서 구한다.
$p(\Theta |>_u) $(사후 확률)$\propto p(>_u|\Theta)$(가능도) $p(\Theta)$(사전 확률)
사전 확률과 가능도는 가정과 계산을 통해서 얻을 수 있기 때문에 사후확률을 수식으로 표현할 수 있다. 사후확률을 최대화하면 정보를 잘 나타내는 파라미터를 추정하게 된다.
- 사후확률 : posterior
주어진 유저의 선호 정보에 대한 파라미터의 확률 - 사전확률 : prior
학습할 파라미터에 대한 사전 정보 확률
어떤 분포를 따른다는 가정을 통해 나타내는데 보통 정규분포를 사용한다.
우리가 사용하는 학습 파라미터는 벡터이기 때문에 정규분포도 행렬로 정의한다.- 평균 : 0
- 공분산 행렬 $\sum_{\theta} = \lambda_{\Theta}I$
※$I$ = 단위행렬
모델링 할 때 정의하는 하이퍼 파라미터이다
공분산 행렬의 크기($\lambda_\Theta$)가 정규화 역할을 수행한다.
- 가능도 : likelihood $p(>_u|\Theta)$
파라미터를 고정했을 때 유저의 선호 정보 확률
MF의 예측 수식이 사용된다.
유저가 item i를 item j보다 선호할 확률을 MF 수식을 사용해서 표현한다. 확률은 0~1 사이이기 때문에 sigmoid($\sigma(x):=\frac{1}{1+e^{-x}}$)를 사용한다. 최종적으로 유저 u가 item i가 j보다 선호할 확률을 모두 곱한 값이 전체 data에 대한 likelihood가 된다.
$$\prod_{u\in U}p(>_u|\Theta) = \prod_{u, i, j\in D_s}p(i>_u j)=\prod_{u, i, j\in D_s}\sigma(\widehat{x_{uij}}(\Theta))$$- $\widehat{x_{uij}}$
MF에 의한 평점 예측에 의해서 유저 u의 item i에 대한 평점 예측값과 item j에 대한 평점 예측값의 차 - $\widehat{r}_ui$
유저 u의 item i에 대한 평점 예측값 - $\widehat{r}_uj$
유저 u의 item j에 대한 평점 예측값
- $\widehat{x_{uij}}$
BPR 목적함수
BPR-OPT $:= \ln p(\Theta | >_{u}) = \displaystyle\sum_{(u,i,j)\in D_{s}} \ln \sigma(\hat{x}_uij)-\lambda_{\Theta}\parallel\Theta\parallel^2$
뒤의 $\theta_{\Theta}\parallel\Theta\parallel^2$ term이 L2 regularization처럼 작동하고
앞의 term $\displaystyle\sum_{(u,i,j)\in D_{s}} \ln \sigma(\hat{x}_uij)$이 likehood이다.
LearnBPR
목적함수는 미분가능하기 때문에 학습파라미터로 gradient를 구해 GD를 수행할 수 있다.
$$\frac{\partial BPR-OPT}{\partial\Theta} = \displaystyle\sum_{(u,i,j) \frac{\partial}{\partial\Theta} \in D_{s}} \ln \sigma(\hat{x}_uij)-\lambda_{\Theta}\frac{\partial}{\partial\Theta}\parallel\Theta\parallel^2$$
$$\Theta \leftarrow \Theta -\alpha\frac{\partial BPR-OPT}{\partial\Theta}$$
하지만 이 문제에서는 일반적인 GD가 적절하지 않고 Learn BPR을 사용해야한다. Learn BPR은 bootstrap기반의 SGD이다.
유저의 선호정보를 사용하여 만든 학습정보
$D_s:= \{(u,i,j)|i\in I_u^+ \wedge j\in I \backslash I_u^+ \}$를 사용한다.
보통 관측한 아이템<관측하지 못한 아이템 이기 때문에 모든 학습데이터를 사용하면 학습의 비대칭이 발생한다. 그래서 이것을 triples단위로 랜덤 샘플링해서 사용한다.
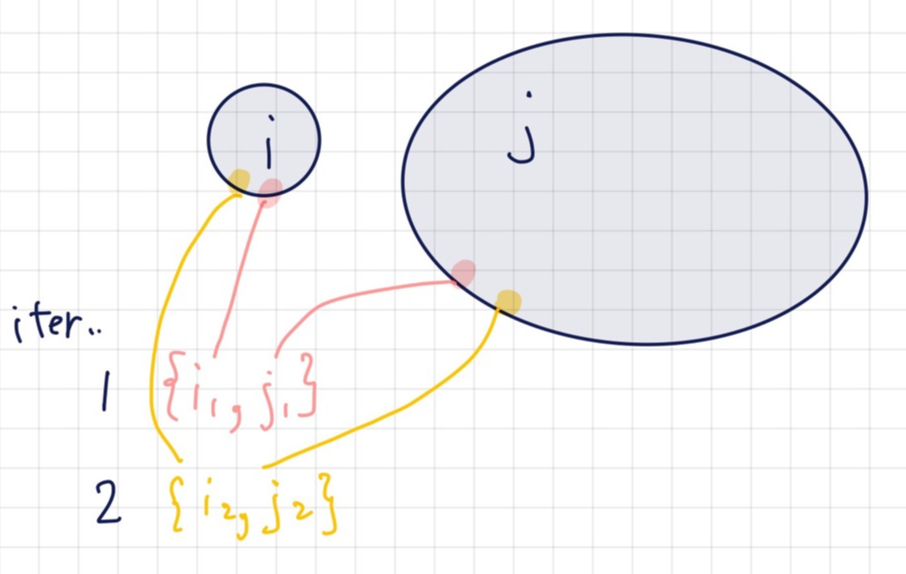
그래서 선호하는 아이템 i 하나, 선호하지 않는 아이템 j 하나를 동일한 weight로 sample해서 동일한 u, i 가 계속 등장하지 않게 한다.
그래서 Learn BPR을 MF모델에 적용하면 학습 파라미터인 $p_u$와 $q_i$를 업데이트 해야한다.
그래서 $p_u$와 $q_i$에 따라서 수식이 다음과 같아진다.




