NBCF의 한계
- Sparsity(희소성) 문제
- 데이터가 충분하지 않다면 추천성능이 떨어진다.
유사도 계산이 부정확하기 떄문에 성능도 떨어진다. - 데이터가 부족하거나 혹은 아예 없는 유저, 아이템의 경우 추천이 불가능하다. (Cold Start)
- 데이터가 충분하지 않다면 추천성능이 떨어진다.
- Scalability(확장성) 문제
- 유저와 아이템 수가 늘어날수록 유사도 계산도 늘어나 시간이 오래 걸린다
- 하지만 데이터양이 많아지기 때문에 정확한 예측을 한다.
MBCF : Model Based Collaborative Filtering
항목 간 유사성을 비교하는 것에서 벗어나 데이터에 내재한 패턴을 이용해 추천하는 CF기법
- SVD
- Matrix Factorization
- Deep learning
| NBCF | MBCF |
| non parametric 파라미터를 학습하지 않는다 |
parametric 파라미터로 학습한다 |
| memory based 데이터를 그대로 메모리에 올려놓고 collaborative filter를 사용한다 |
model based 유저 벡터와 아이템 벡터는 모두 학습을 통해 계속 변하는 파라미터로 이루어진다 |
| 유저-유저, 아이템-아이템 간의 유사성을 비교 | 데이터에 숨겨진 특성을 찾는다. |
| 데이터는 학습에만 사용하고 모델에 학습 내용이 저장되어 있기 떄문에 다시 데이터를 매번 학습할 필요가 없어서 서빙 속도가 빠름 |
|
| sparsity ratio<=99.5% 일 때만 사용 | sparsity ratio가 99.5%을 넘어도 사용 |
| 사용자, 아이템 개수가 많이 늘어나도 성능이 좋다 | |
| 전체 데이터에 대해 학습하지 않고 특정 주변 이웃에게만 영향을 받는다 | 전체 데이터의 패턴을 학습하지 않아 overfitting 되지 않는다. |
| 공통의 유저나 아이템을 많이 공유해야만 유사도 값이 정확해진다. 적당히 coverage가 비슷한 데이터들은 많지 않기 때문에 성능도 높아지기 힘들다. | 특정 유저나 아이템의 유사도를 직접 계산하지 않아 Limited Coverage가 없다 |
MBCF에서는 주어진 데이터로 모델을 학습하면서 정보들이 파라미터로 압축되고, 모델의 파라미터는 데이터의 패턴을 나타내고 이 파라미터는 최적화를 통해 업데이트 된다.
Implicit Feedback vs Explicit Feedback
| Explicit Feedback | Implicit Feedback |
| 선호도를 직접적으로 알 수 있는 데이터 | 유저의 선호도를 간접적으로 알 수 있는 데이터 |
| 영화평점, 맛집 별점 | 클릭 여부, 시청 여부 |
| 데이터의 양이 훨씬 많다. 수집하기 더 쉽다. | |
| 평점을 예측한다. | 얼마만큼 선호할지, 얼마만큼 선호하지 않을지를 예측하게 된다. |
Latent Factor Model
latent=embedding
유저와 아이템 관계를 잠재적 요인으로 표현할 수 있다고 보는 모델
관계를 몇 개의 벡터로 compact/dense하게 표현한다.
유저-아이템 행렬을 저차원의 행렬로 분해하는데 그 저차원의 행렬은 생성되긴 하지만 의미를 표면적으로는 알기 어렵다.
유저와 아이템을 같은 차원으로 latent하게 만들어서 같은 공간에 embedding하게 될 경우, 유저 벡터와 아이템 벡터가 같은 공간에 놓여 유저와 아이템 사이의 유사한 정도를 확인할 수 있다. 그 두 벡터가 유사하게 놓인다면 추천될 확률이 높아진다.

이렇게 같은 차원에 놓이게 되는데 여성향, 남성향과 같은 축에 대한 설명은 원래 알 수 없고 잠재적이다.
Singular Value Decomposition : SVD
2차원 행렬을 분해하는 기법
추천시스템에서 사용하는 데이터는 유저-아이템으로 이루어진 2차원 rating 행렬(=Rating Matrix R)이다.
R을 유저와 아이템의 잠재요인을 포함할 수 있게 분해하면 3가지 행렬이 나온다
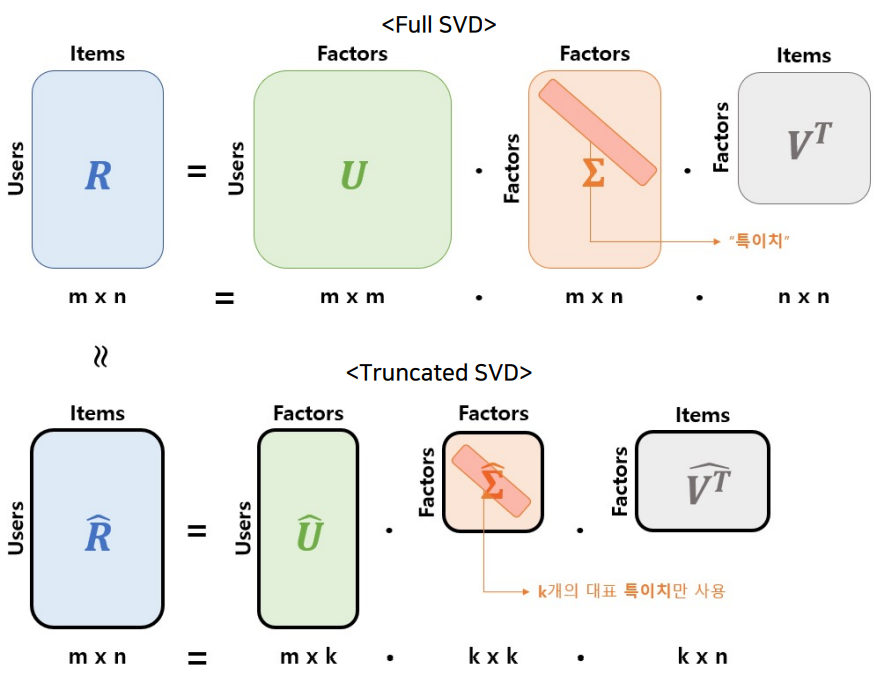
- 유저 잠재 요인 행렬 U
한 user에 대한 벡터는 m크기를 가지며 행으로 들어간다. - 아이템 잠재 요인 행렬 V
아이템 전체 갯수인 n차원으로 이루어지며
한 아이템에 대한 벡터는 n크기를 가지며 열로 들어간다. 전치 되어 있기 때문에 열로 들어간다. - 잠재요인 행렬 $\Sigma$
U와 V의 차원이 맞지 않기 때문에 가운데의 잠재요인 행렬이 맞추어준다. 각 factor의 중요한 요소들로 이루어진 latent vector가 대각으로 들어간 대각행렬이기 때문에 대각선에 있는 원소를 빼고는 다 0으로 이루어져 있다.
세 행렬을 다 곱했을 때 원래 행렬 R로 복원할 수 있다.
- Full SVD
R을 3개의 행렬로 온전하게 분해하는 것 - Truncated SVD
Full SVD를 압축한 것
Latent Vector 가운데에서 대표값으로 사용할 특이치를 k개 뽑아서 그 특이치들에 따라서 user matrix와 item matrix도 압축된다.
압축된 행렬은 원래 행렬 R과 완벽히 같지는 않지만 최대한 유사하게 복원할 수 있다
그래서 Truncated SVD를 이용하면 몇 개의 특이치만을 가지고도 유용한 정보를 유지할 수 있다. 이는 정보가 요약되는 효과를 가져온다. $\hat{R}$은 부분 복원되었긴 했지만 가장 중요한 정보들은 남아있게 된다. 그래서 추천시스템에서 $\hat{R}$은 예측값으로 사용한다.
SVD의 한계
전통적 SVD는 한계가 있다.
- 분해하려는 행렬의 knowledge가 불완전할 때 SVD가 작동하지 않는다.
실제 user-item matrix는 sparse하고 결측치가 많아서 SVD를 수행할 수 없다. - SVD는 모두 채워져 있어야 수행되기 때문에 결측된 entry를 채우는 Imputation을 통해 dense하게 만든다
0이나 평균으로 채우는데, 그건 데이터양을 증가+왜곡 시킨다. 결과적으로 예측 성능이 줄어들게 된다. - 특히 행렬의 entry가 매우 적을 때는 과적합 되기 쉽다.


