기계학습과 딥러닝은 확률론을 기반으로 해서 이해하려면 확률론을 알아야 한다.
예를 들어, 학습시 필요한 loss fuction (손실함수)는 데이터공간을 통계적으로 유도하기 때문에 중요하다.
확률분포
데이터를 표현하는 초상화
확률분포를 한 번에 구하기는 불가능하다. 그래서 기계학습 모형으로 이 확률분포를 추론하게 된다.
추론하는 데이터 공간을 $\mathscr{X} \times \mathscr{Y}$ 로 표기한다.

확률변수
우리가 관측하는 실제 데이터는 확률변수로 표기한다.
확률변수 $(\textbf{x},y) $ 는 $\mathscr{X} \times \mathscr{Y}$의 원소이다
$$ (\textbf{x},y) \in \mathscr{X} \times \mathscr{Y}$$
확률변수는 함수로 생각하면 되는데, 임의로 우리가 데이터 공간에서 관측하게 되는 함수이다.
데이터를 추출할 때 확률변수를 사용한다.
확률변수로 추출한 데이터의 분포를 $\mathscr{D}$라고 한다.
$$ (\textbf{x},y) \sim \mathscr{D}$$
확률변수는 데이터 공간 $\mathscr{X} \times \mathscr{Y}$ 에 의해 결정되는 것이 아니다.
실제 존재하는 데이터들의 확률분포이다.
확률분포$\mathscr{D}$에 따라 이산, 연속확률변수가 구분 된다. 다른 확률변수도 있다.
- 이산확률변수 (discrete)
확률변수가 가질 수 있는 경우의 수를 모두 고려해서 확률을 더한다.
$$ \mathbb{P} (X \in A )= \sum_{\textbf{x} \in A} P(X=\textbf{x}) $$
다시 말하면 이산확률변수는 확률변수$X$ 가 $\textbf(x)$를 가질 확률들을 모두 더한 것이다.
이 함수를 확률질량함수라고 한다 - 연속확률변수 (continuous)
밀도함수$P(\textbf{x})$를 적분해서 그 확률변수의 확률을 구할 수 있다
밀도함수는 누적확률분포의 변화율을 가지고 만든 것이지 밀도가 확률이 아니다.
$$ \mathbb{P} (X \in A )= \int_{A} P(\textbf{x})d\textbf{x} $$
그래서 적분해야 확률분포값을 알 수 있다
결합분포 Joint distribution
동일한 표본공간에서 정의 되는여러 확률변수를 한 분포로 합쳐서 고려하는 분포라고 생각한다.
전체 데이터 공간 $\mathscr{X} \times \mathscr{Y}$에서의 분포
$$P(\textbf{x}) ,y)$$
여기에서 $\mathscr{X}$와 $\mathscr{Y}$를 같이 고려한 것이다
그림 1 에서 y의 값, x의 값에 빨간 칸으로 나뉘고 칸마다 따라서 속하게 되는 파란 점들이 있다.
그러면 각각의 칸에 대해서 이산확률분포처럼 생각할 수 있다.
결합분포를 결정할 때는 원래 확률분포에 상관없이 정할 수 있다.
ex) 이산 -> 연속, 연속->이산
주어진 데이터의 모양을 보고 어느 분포로 결합분포를 상정할지 적절히 선택하면 된다.
주변확률분포 Marginal distribution
$textbf{x}$의 값에 따른 빈도를 센다. $y$는 고려하지 않는다.
그래서 전체 $y$에 대해서 해당 x에 해당하는 칸에 속하는 만큼 세어준다.
그 점들의 x의 값에 따른 빈도를 세서 분포를 만든다.

주변확률분포는 결합확률분포를 각각의 $y$에 대해서 더해주거나 적분해주면 구할 수 있다.
$$P(\textbf{x},y)=\sum{y}P(\textbf{x},y)$$
- $\textbf{x}$에 대해서 덧셈이나 적분을 하면 $y$에 대한 주변확률 분포를 구할 수 있다
- $y$에 대해서 덧셈이나 적분을 하면 $\textbf{x}$에 대한 주변확률 분포를 구할 수 있다
위의 그림 예시와 같은 경우이다.
조건부 확률분포
- $y$가 주어져 있는 상황에서 $x$에 대한 확률분포
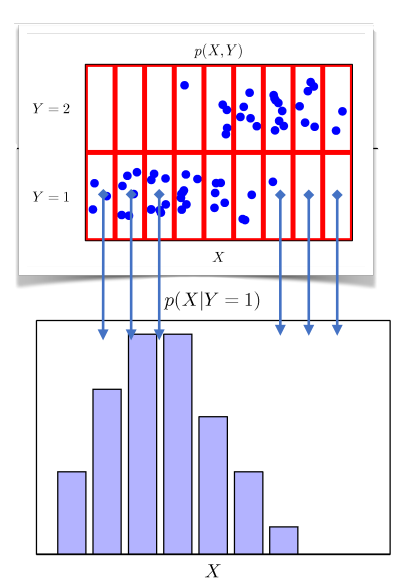
위의 사진은 y가 1인 경우에서만 x를 세어서 확률분포를 구했다.
y=1인 조건에서의 확률분포라고 말할 수 있다.
특정 클래스의 확률분포를 보여주기 때문에
예측 모형을 세울 때 우리가 보고싶은 관점에 따라서 데이터를 볼 수 있다.
그래서 명확하게 통계적 모델링을 하는데 확률분포가 도구가 될 수 있다.
조건부확률 $P(y|\textbf{x})$
입력변수 $\textbf{x}$가 주어졌을 때 정답이 $y$인 확률(continuous일 경우는 밀도)
= x가 주어졌을 때 y의 확률
보통 ML/AI 등 학습에서 주어진 데이터x에 대해서 정답일 확률을 계산하는 용도으로 자주 사용된다.
그래서 데이터 x로부터 추출된 특징패턴 $\phi(\textbf{x})$과 가중치행렬 $\textbf{W}$을 통해 조건부 확률을 계산한다. 그것을 분류문제에서 softmax($\textbf{W}\phi + \textbf{b}$)이다.
※특징패턴은 딥러닝 다층신경망을 사용해서 추출한다
$$P(y|\textbf{x}) = P(y|\phi(\textbf{x}))$$
회귀문제는 보통 연속확률변수를 다룬다.
그래서 밀도로 해석을 하는데 조건부 확률 대신 조건부 기대값 $\mathbb{E} [ y | \textbf{x} ]$ 을 구해서 정답을 추론한다.
확률밀도함수이기 때문에 적분을 해야한다.
$$ \mathbb{E} [ y | \textbf{x} ]=\int_{y}y{P}(y|\textbf{x})dy$$
※$P(y|\textbf{x})$:조건부 확률밀도함수
이 조건부 기대값은 L2 norm( $\mathbb{E} \parallel{y}-f(\textbf{x})\parallel_{2}$ )을 최소화 하는 함수와 일치한다.
기대값(=평균) expectation (=mean)
데이터를 대표하는 대표적인 통계량
확률분포를 통해 다른 통계적 범함수를 계산하는데 사용된다.
기계학습에서는 평균의 의미보다 넓게 사용된다.
데이터 해석시에 사용한다.
- 연속확률분포
$$\mathbb{E}_{\textbf{x} \sim P(\textbf{x})}[f(\textbf{x})]=\int_{x}f(\textbf{x})P(\textbf{x})d\textbf{x}$$
연속확률분포는 주어진 함수 $f(\textbf{x})$에 확률밀도함수를 곱해서 적분한다 - 이산확률분포
$$\mathbb{E}_{\textbf{x} \sim P(\textbf{x})}[f(\textbf{x})]=\sum{\textbf{x}\in X}f(\textbf{x})P(\textbf{x})$$
이산확률분포는 주어진 함수 $f(\textbf{x})$에 확률질량함수를 곱해서 모두 더해준다(summation).
기대값으로 계산할 수 있는 여러 통계랑
- 분산

- 첨도(Skewness)

- 공분산
두 개의 확률변수에 대해서 계산한다.
몬테카를로 샘플링
기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 많다.
그렇다면 기대값이나 기대값을 활용한 다른 통계량들도 알 수 없다.
그럴 때는 데이터를 이용해서 기대값을 계산해야 한다.
어떤 데이터를 쓸지를 뽑는 것이 샘플링이다.
샘플링한 데이터로 기대값을 대신 계산해볼 수 있다.
$$\mathbb{E}_{\textbf{x} \sim P(\textbf{x})\approx \frac{1}{N}\sum^{N}_{i=1}f(\textbf{x}^{(i)}) }$$
샘플링한 데이터을 $f(\textbf{x})$ 에 넣고 그것들의 산술평균이 기대값에 근사하게 된다.
확률변수가 이산형이든 연속형이든 상관없이 몬테카를로 샘플링을 할 수 있다
대수의 법칙 Law of large number
샘플링을 독립적으로 해야지만 작동한다는 점이 중요하다.
독립성이 보장된다면 대수의 법칙에 의해 수렴성이 보장된다.
'부스트캠프 AI Tech 3기 > 이론 : U-stage' 카테고리의 다른 글
| [Day5] AI math 8. 베이즈 통계학 맛보기 (0) | 2022.01.22 |
|---|---|
| [Day4] AI math 7. 통계학 맛보기 : 모수, 확률분포, 정규분포,최대가능도 추정법, MLE, 로그가능도, 확률분포 거리, 쿨백라이블러 발산 (0) | 2022.01.22 |
| [DAY4] AI math 5. 딥러닝 학습방법 이해하기 (0) | 2022.01.20 |
| [DAY3] AI math 4. 경사하강법 -2 (0) | 2022.01.20 |
| [DAY3] AI math 3. 경사하강법 -1 (0) | 2022.01.20 |



